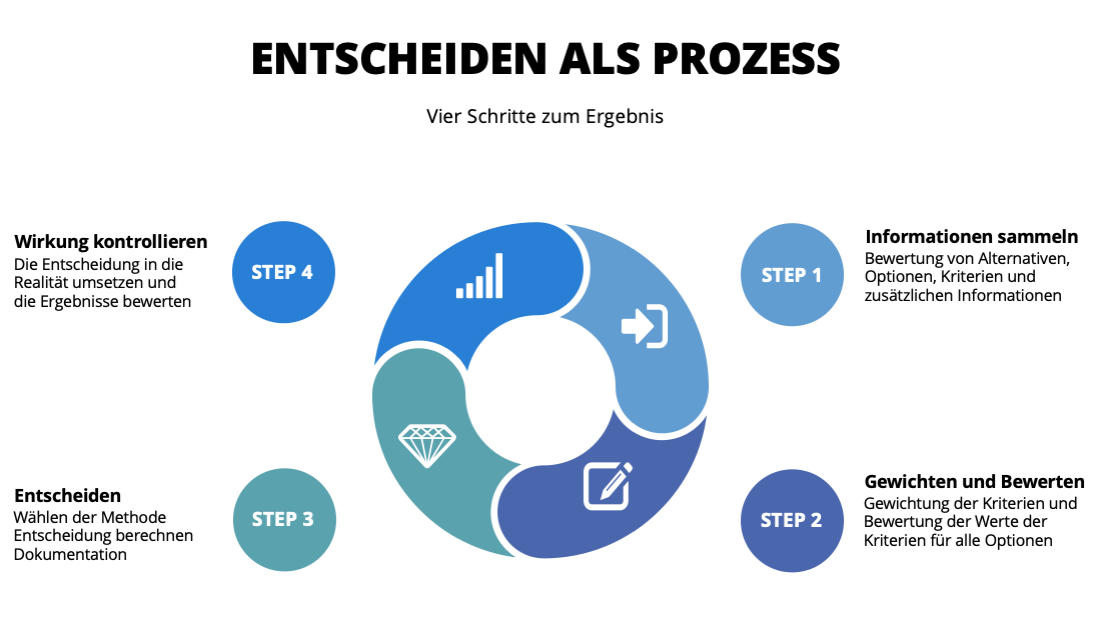
Was hat es mit Entscheidungen auf sich?
Entscheidungen bilden die Grundlage menschlichen Handelns. Argumente brauchen wir nur, um Entscheidungen zu treffen oder zu erklären. Entscheidungen betreffen nicht nur uns selbst, sondern auch andere Menschen. Deshalb sind Entscheidungen so wichtig.
Entscheidungen werden oft im Hintergrund, privat oder sogar im Geheimen getroffen. Das ist in Ordnung so, doch wenn es um andere Menschen geht, ist Transparenz von Vorteil. Transparenz schafft Vertrauen. Die Demokratie braucht Vertrauen, ebenso wie ein Arzt oder ein Rechtsanwalt.
Wie würden Sie darüber denken, wenn die Entscheidungsprozesse von Politikern, Ärzten oder Rechtsanwälten vorliegen würden, mit Gewichtungen, Argumenten (bewerteten Kriterien) und den möglichen Optionen. Und das sauber ausgerechnet und dokumentiert?
Wäre das nicht außerordentlich? Und das kann für viele Bereiche im Leben gelten.
Apropos Leben: Das Leben geht weiter und neue Optionen tun sich auf und auf einmal gelten neue Bewertungskriterien. In diesem Fall ist es gut, wenn wir eine „alte“ Entscheidung aufrollen können, diese neuen Faktoren ergänzen können, und die Entscheidung erneut überprüfen können. In den meisten Fällen bleibt es übrigens beim gleichen Ergebnis.
Doch wie treffen wir Entscheidungen? Und wie steht es mit dem berühmten Bauchgefühl, das so oft anders ist als eine technisch berechnete Entscheidung? Hierfür gibt es eine Lösung.
Methoden zur Entscheidungsfindung gibt es viele. Sehr viele sogar. Wir haben uns auf zwei grundlegende Methoden konzentriert: Die so genannte „Nutzwert-Analyse“ und den so genannten „Paarweisen Vergleich“. Beide Methoden könnten unterschiedlicher nicht sein.
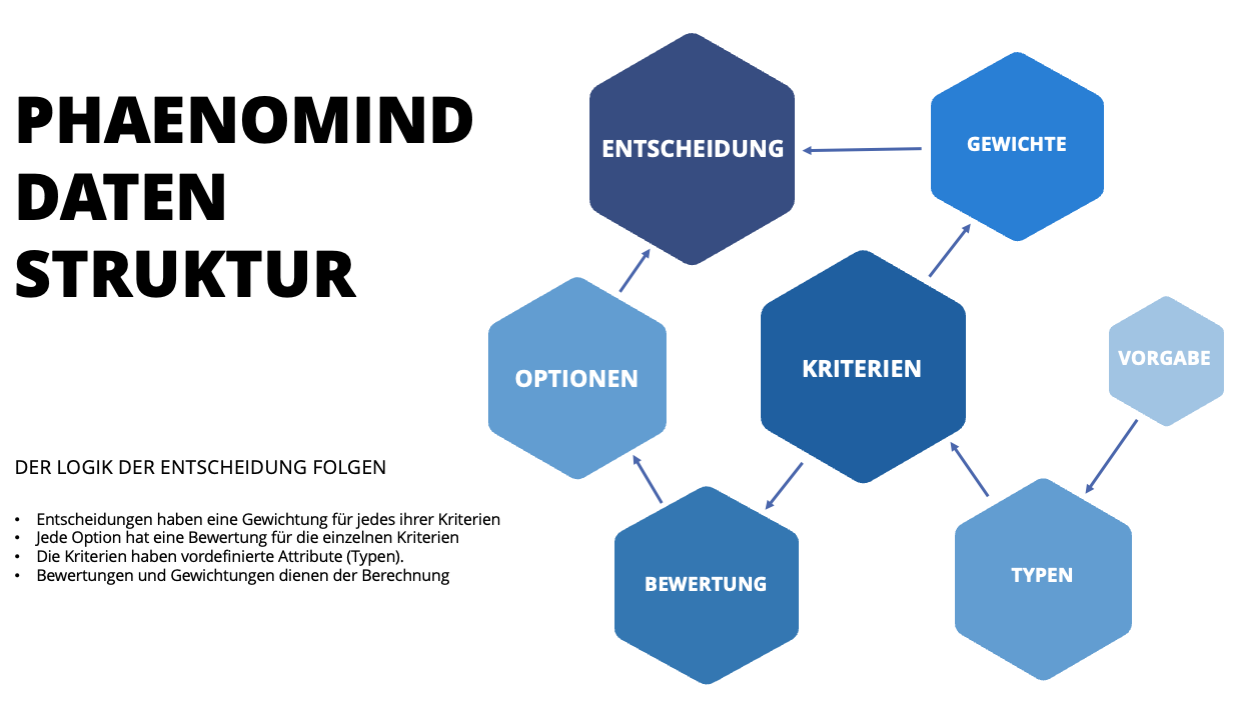
Die Nutzwert-Analyse (im englischen Cost Utility Analysis) ist eine rein technische Analyse der vorliegenden Kriterien für alle Alternativen oder Optionen. Es werden Kriterien ermittelt und pro Option gefüllt. Also zum Beispiel bei Autos der Verbrauch oder die Größe des Innenraums. Diese können dann normiert werden damit nicht Äpfel mit Birnen verglichen werden. Und dann können diese Kriterien priorisiert werden, sie werden also in eine Reihenfolge gebracht. Danach kann man für jede Option einen Wert ausrechnen - und der höchste Wert gewinnt, ist also die beste Wahl. Diese Kriterien der Nutzwert-Analyse sind quantitative Werte, also Zahlen, die wir angeben können, weil sie eine Messgröße darstellen.
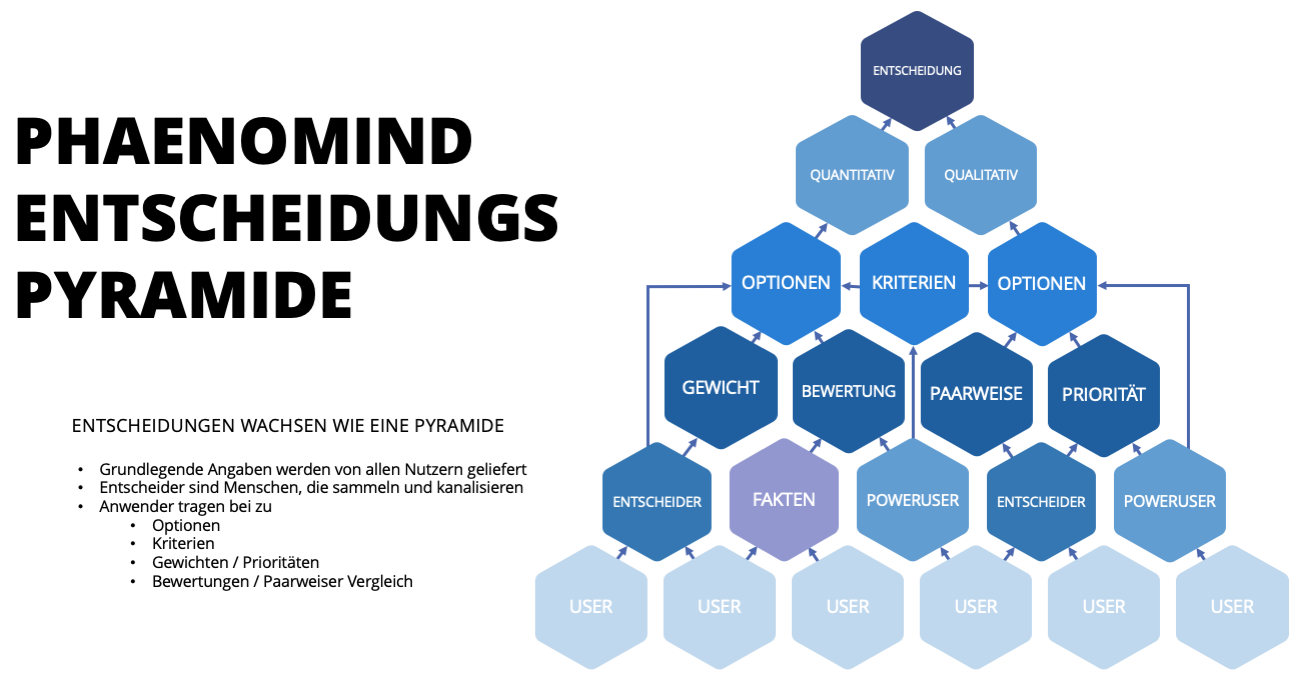
Ganz anderes beim Paarweisen Vergleich (im englischen Analytic Hierarchy Process, AHP): Hier werden zunächst alle Optionen einander gegenübergestellt und in Hinsicht auf ein Kriterium gegeneinander abgewogen. Das hört sich kompliziert an? Ein Beispiel: Drei Bewerber werden zum Thema Sympathie beurteilt. Da gibt es keine Zahl, die man verwenden könnte. Aber ein direkter Vergleich ist möglich: A ist sehr viel sympathischer als B und C ist ganz leicht sympathischer als B. Diese Vergleiche führen wir für alle nicht messbaren Kriterien durch. Danach wägen wir die Kriterien ebenfalls gegeneinander ab. Also Sympathie ist leicht wichtiger als Sprachkenntnisse, aber Fachkenntnisse sind sehr viel wichtiger als Sympathie.
Aus beiden Bewertungen kann dann ein Ergebnis berechnet werden. Dieses Ergebnis entspricht in den meisten Fällen dem Bauchgefühl. Es nennt sich qualitative Bewertung.
Und wenn das „echte“ Bauchgefühl nicht zum Ergebnis passt? Dann haben Sie etwas falsch gemacht: Sie haben Kriterien nicht mit eingebracht oder Sie haben falsch bewertet.
Am Ende haben wir also zwei Ergebnisse: Eines aus der quantitativen Bewertung und eines aus der qualitativen Bewertung. Diese kann man jetzt gegenüberstellen und gewichten, also zum Beispiel 60% qualitativ und 40% quantitativ. Dann überwiegt das Bauchgefühl.
Interessant wird es, wenn wir ein paar Sachen ausprobieren:
- Verschieben der beiden Ergebnisse gegeneinander
- Verändern der Bewertung der qualitativen Kriterien
- Verändern der Priorisierung der quantitativen Kriterien
So können wir dann feststellen, wann eine Entscheidung „kippt“, also ein anderes Ergebnis berechnet wird. Da kann man was draus lernen - meistens aber bleibt es beim ersten berechneten Ergebnis.